平时总会跟大家瞎聊一些东西,这时候发现有的人想聊哲学,有的人想聊物理,我思考了很久就找到了“时间”这个话题。
其实不管是生活中,还是科学理论和技术实践上,都有许多跟时间有关的事情,这些是可以串起来聊一聊的。
不过此文很长,并且有点“凌乱”,最后可能会让人觉得其实只是“好像一些没啥用的知识又增加了”。
时间是什么?
首先从哲学开始,先理清一下“哲学”的概念——哲学是研究普遍的、基础问题的学科。
我对哲学的理解,简单地说是,人类的“意识”对“物质”世界产生的“认知”,最终形成了对各种事物在我们脑海里所对应的“概念”,并且通过“归纳”、“演绎”等方式最终形成了“逻辑”与“知识”。
哲学当然是普遍的,例如大量的人可能不需要太多的交流,也能达成相近的哲学意识。但是哲学又是个性化的,每个人也可以有自己的“哲学”。
那“时间”在哲学里是个什么概念呢?
时间似乎是一个人出生之后就不言自明的“概念”了。
但细细想来,我不知道准确的答案,而且似乎哲学上也没有准确的定义。
当我搜索Wikipedia时,就发现这样一句话:“长久以来,时间一直是宗教、哲学及科学领域的研究主题之一,但学者们尚且无法为时间找到一个可以适用于各领域、具有一致性且又不循环的定义”。
对“时间”这个概念,是不是感受到好像没有那么简单了。
生活时间
人的知识首先来自于生活常识
时间的感知
如果回到最基本的概念上,尽量不预设任何的知识,让我们想一想人是如何感知到“时间”的呢?
人们常常会说“世界好安静,仿佛时间都停止了”,也就是说一个静止的世界会让人感受不到时间的存在。
反之,如果坐在马路边,当看着小汽车一辆辆地驶过、看着工地上将楼房一层层加高,时间好像在发生作用了。
如果有人拿出同一个地点的两张照片,当它们长得一模一样或者说连“找茬”也发现不了任何区别,那么一般来说这两张照片应该是在同一个时间拍摄的。
反之,如果发现了一些区别,或者说照片里的某些元素发生了变化,人就能从这些变化中感知到时间的流逝。
所以虽然我不能给时间一个很好的定义,但我们都可以确信——时间是对物质世界变化的一种感知。
对于这样一次的“变化”,我们可以称之为“事件”。
事件的发生是与某个具体的时间相关联、相对应的。
多个事件的发生有先后顺序,也就是在时间上有“早晚”的概念。
(更准确地说,这个时间的比较应该是在同一个地点上发生的事件,或者是在同一个地点上观察到的事件。)
这样可以明确时间的一个重要特性——传递性,即在时间上对多个事件早晚关系之间的比较是可以依次传递的。例如,假设A比B早、B又比C早,那就一定有A比C早。
时间的传递性看起来是理所当然的,但这是一个很重要的数学性质。
因为这表示时间在拓扑结构上应该没有“成环”,而是一条“线”。
如果可以明确一个方向,即是“射线”,一般称它为“时间轴”。
时间的度量
那如何度量时间呢?
远古的人类看着太阳早起晚落,才有了“一天”的时间概念。另一方面,人们很难把“打到一只猎物”这种不确定的事件作为一种时间的衡量维度。
其实我们能够发现,身边有很多“事件”在周而复始的发生,即周期性的事件,就可以用它们来度量时间。
好比地球绕太阳公转一周,即地球上四季的一轮变化,可以算作1年。
月球绕地球公转一周,也就是月亮一轮阴晴圆缺,可以算作1月。
当然还有地球自转一周,即太阳东升西落到再次升起,可以算作1日。
人们就这样通过各种各样自然界的周期性事件,建立了对时间的度量维度。
如果可以对周期性事件的发生次数进行计数,就可以得到一种对时间的计量,例如第几天、第几年等等。
当然因为周期时间的尺度不同,这就是在不同的量级上为时间建立了不同的测量方法。
这样在时间轴上就定义了“刻度”,也就是给了每一个物理上发生的事件一个明确的时间坐标,这样也能很方便地辨识两个事件的早晚了。
在有了度量方法的基础上,可以注意分辨一下语言可能带来的歧义,即时间其实有两个涵义“时刻”和“时段”。
时刻在时间轴上是一个点,代表一个具体的事件发生时间点,而时段则是一个线段,是两个事件的间隔时间区间,或者表示一个事件持续发生的时间长度。
在生活语言中,我们往往对这两个涵义不加区分,例如“你今天什么时间去晚饭?”表示的是时刻,而“你今天下午有时间讨论一下吗?”更多表示的是时段(如果你3点零5分有事情,那一般不会回答自己3点有空吧)。
现在分清了时间的这两个语义,就可以更明确地讨论一些问题。例如产品运营上常常提出一些需求,比如“我们要做一个随时间变化的新增用户数看板”,这句话里的时间是哪个意思呢?
这里其实至少包含了三个“时间”:首先有一个“时刻”是看板的横轴刻度,其次有一个“时段”是看板的起止时间(绘图区间),最后还有一个很隐蔽的“时段”是对新增用户数的统计时长。
如果把统计时长分得很小(例如每秒就统计一次),那在这个时段内的新增用户数大概率其实是零的,也就没有数据,这种图画出来是很不好看的。
既然要指出是对每小时或者每天的新增用户数进行统计,这句话蕴含的精确意思可能是“以日期为横坐标,做一个近三个月的每日新增用户数看板”。
历法
到这里为止,其实都是一些对生活时间的简单常识了,现在可以稍微深入下去,想点复杂一些的事情了。
回到年月日的讨论中来,也就是在常识上地球绕太阳一周是1年、地球自转一周是1天,大家肯定觉得是没有什么问题了。
但是一个很不巧(其实是必然)的事情是,1年并不是1天在时间上的整数倍。
更复杂地是,精确地现代观测发现,其实“年”还至少有两个不同的概念,一个叫回归年,一个叫恒星年。
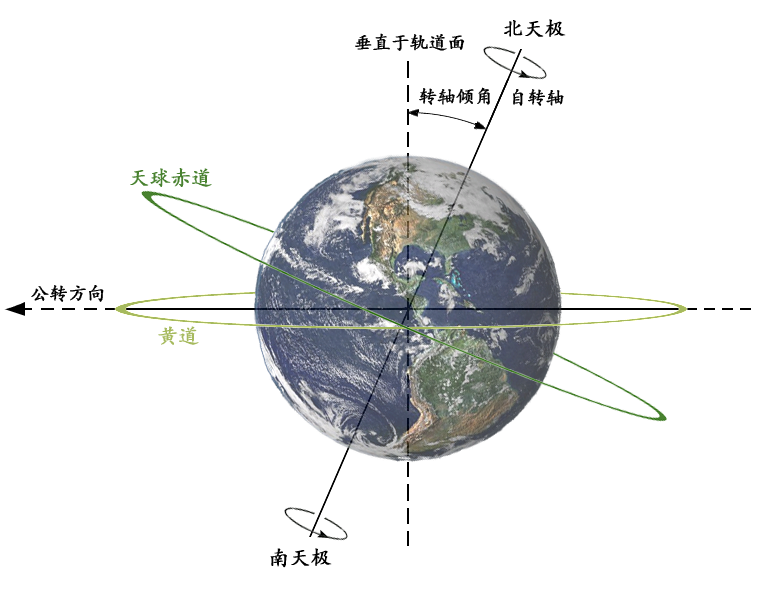
回归年是站在地面观察者(也就是我们日常生活)的角度看到的1年,指太阳连续两次通过春分点的时间间隔。
我们想象有一个与地球同球心,并有相同的自转轴,半径无限大的球,称为“天球”。
地球的自转可以投影出“赤道”,而地球绕太阳公转的轨道面截天球所得的圆称为“黄道”。
黄道和赤道有两个交点,而“春分点”指的就是太阳从南向北在黄赤道上的交点。
即太阳的中心自西向东沿黄道从春分点到下一个春分点所经历的时间,是一个回归年,又称为太阳年。
1回归年有365.2422日,即365天5小时48分46秒。
恒星年是地球公转的真正周期,是在太空的角度看到的1年,从太阳上看,地球中心从太空中的某一点出发,环绕太阳一周,然后又回到了此点。
如果从地球上看,则是太阳中心从黄道上的某一点(可以对应某一颗遥远的恒星)出发,运行周天,然后又回到了同一点(同一恒星)。
1恒星年约为365天6时9分10秒。
因为地球的自转轴方向其实不是保持不动的,这个运动称为“进动”。
关于进动,可以想象一个陀螺,它在自转的同时,自转轴也在转动。
1个恒星年会比1个回归年要长大约10分钟,这个时间被称为“岁差”,也就是说大约每过140个恒星年会比相应的回归年多过了1天的时间。
那日历上的“年”,是按哪个“年”来的呢?显然是基于回归年,因为我们的古人只在地球上生活,太阳的光照是最直观也最重要的感知。
那么如何给某年中的某天一个标记,就是记录生活时间所要解决的首要问题了。
最简单的办法,从每年开始的第一天依次计数,这样可以记录到第365天算做一年的结束。
这里马上可以发现有两个问题,一是人工计数到365实在是有点不方便而且容易记错,二是既然1年不是1天的整数。
如果扔掉0.2422的小数不管的话,四五年之后,日历上一年的开始就要和它本应该开始的日期差出1天的时间了。
从古至今,无论国内外的哪个文明,最重要的一件事情就是确定“历法”了,也就是根据对天象的观察,确定一套满足日常生活所需要的时间记录方法。
例如,现在国际通用的公历,就是由古罗马的儒略历演变而来。现在公历以耶稣诞生之年作为纪年的开始(称为“元年”),并且把1年分为12个月,其中大月31天、小月30天。
有意思的是,在古罗马时期,著名的凯撒大帝也就是盖乌斯·尤利乌斯·恺撒(Gaius Julius Caesar)要用他的名字赋予他出生的七月(July),而他的继任者盖维斯·屋大维·奥古斯都也以自己的名字命名了八月(August),并且都要求七八月都是大月(31天),最后大家就只好把二月减少至28天了。
为了解决回归年带小数的问题,公历上每4年设置了一个闰日,但是除非年份能被400整除,否则所有的世纪年(能被100整除)都不设闰日。这样公历年的平均长度为365.2425日,就与回归年的实际时长很接近了。
公历是只依照太阳运动以及有关的季节变化来确定的,所以是一种“太阳历”,简称阳历。
有“阳”就有“阴”,只依照月亮运动来确定的历法就称为阴历。
不过中国农历不是简单的“阴历”,因为农历即参照了月亮运动,也合并考虑了太阳的变化,所以其实是一种“阴阳历”。
农历首先根据月相的变化周期,以每一次月相朔望变化为一个月,同时参考太阳回归年为一年的长度,并设置了二十四节气,其中平年为十二个月、闰年为十三个月,大月三十天、小月二十九天。
农历需要通过合理的置闰法,如在19个农历年中加入7个闰年,使得日历上一年的平均天数与回归年的天数相符。
这种在“时间”上的复杂性,使得中国历史上一共产生了超过102部历法。
世界时和时区
当古人只在地球上一个小范围内生活的时候,周围的人都可以共用一个日历。
但随着大航海的发现,地球是一个球体,当然是有时区的。
麦哲伦舰队在环球航行的时候,有一个船员每天都会写日记,当他回国的时候才发现日期“少”了一天。
这就是因为船每天都顺着太阳转动的方向(从东向西)航行,造成了船上的每一天实际上都比陆地上的每一天多了一点点时间,累积下来最终就差出了一天的日期。
现在出国旅行一般都要“倒时差”了,就是因为地球其他地区的“正午”并不一定就是我们当地时间的“正午”,大家以太阳光照判断出来的生活时间是不一样的。
为了能在地球上有一个统一的时间,现在确立了以格林尼治时间为标准时间的“世界时”,同时将地球上每15度设为一个时区(360度除以24小时),不同地区的人也都有了自己的“地方时”,这样总算是解决了地球人类的时差问题。
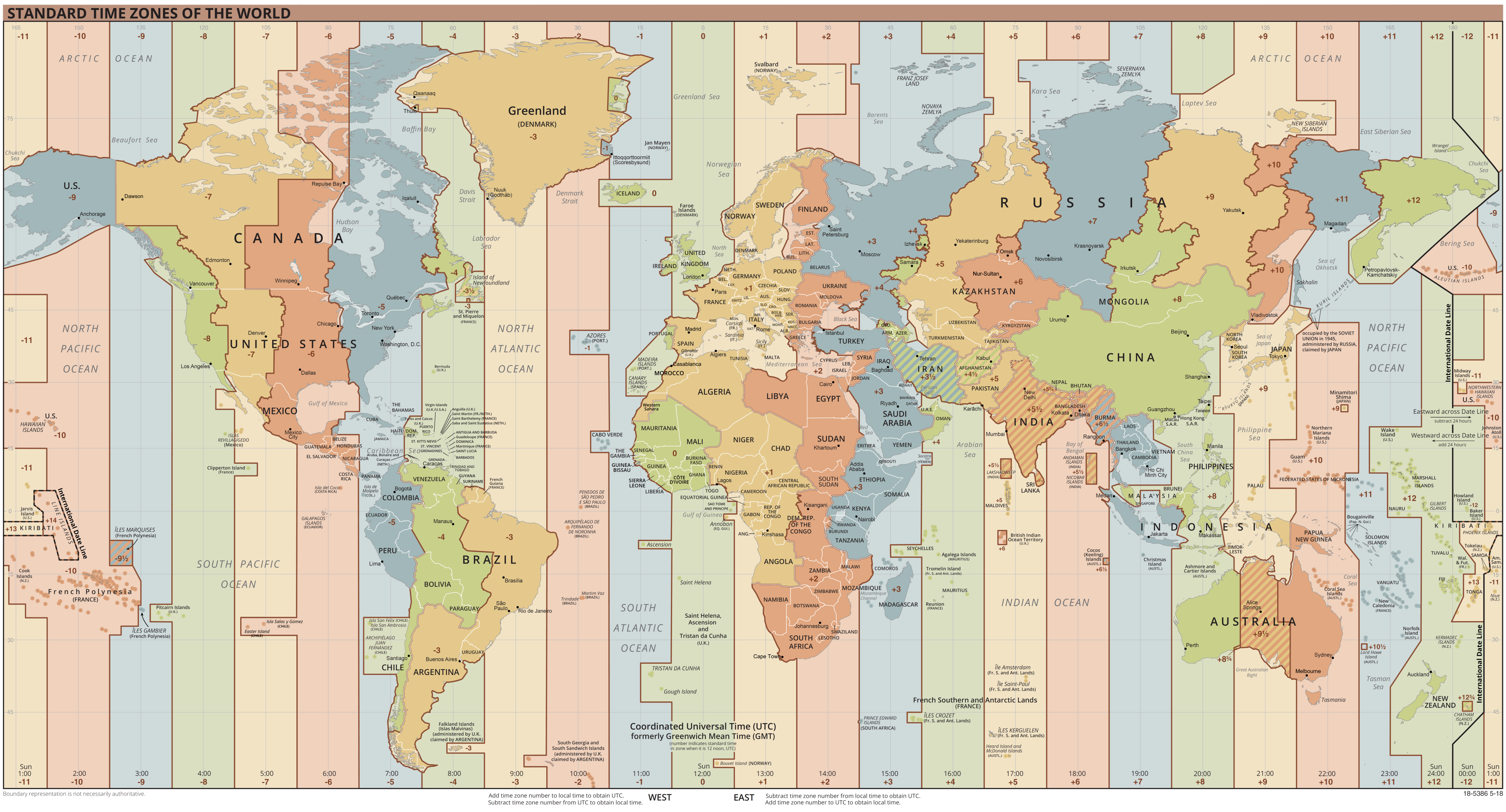
但是人类社会是更加复杂的,真实世界的时区设置不是理论上的那么简单。
比如国际日期变更线,大致上以180度经线为准,但是需要尽量绕开陆地和一些岛屿,并且照顾行政区划的统一。
例如,2011年12月29日萨摩亚把时区从国际日期变更线以东调整到了国际日期变更线以西,而美属萨摩亚却没有跟随调整,此举导致萨摩亚群岛出现了一整日时差。
中国横跨了东五区、东六区、东七区、东八区、东九区5个时区,但却统一使用北京所在的东八区时间。
美国本土分为了4个时区,俄罗斯甚至分成了11个时区。所以有新闻报道了俄罗斯的“高考趣闻”,远东地区都考完了,考生顺手把试题公布到网上,结果欧洲部分的考生还没进考场呢。
物理时间
物理是一门定量的科学
时间单位
现在“秒”是国际单位制中时间的基本单位。秒最初的来源是把1天分成24小时,1小时又分成60分钟,1分钟再分成60秒,即1天=86400秒。
在机械钟表出现之前,要比较精确地测量1秒是不太容易的,因为生活中好像没有这么严格的周期性事件。
在17世纪,摆钟的出现使得人们首次可以精确的计时到秒。
有个有趣的“发现”是,重力加速度差不多就是圆周率的平方,这就与秒摆有关。
因为摆动一下为1秒(即摆动周期为2秒)的摆钟,在标准重力下的摆长“恰巧”很接近1米,那根据单摆周期公式 \(𝑇=2\pi\sqrt{𝑙/𝑔}\)就有\(g\approx\pi^2\)了。
在20世纪初,发明了石英谐振器,是一种利用石英晶片因压电效应而产生谐振现象的原理制成的器件。
压电效应是由雅克·居里(哥哥)与皮埃尔·居里(弟弟,就是居里夫人的老公咯)于1880年发现的。
石英谐振器的频率大致在兆赫兹,也就是可以提供微秒级的时间精度。
现在,已知最精准的时钟是“原子钟”,是基于原子能级间跃迁产生的电磁波来估算时间的。
当前最先进的原子钟时间精度已经达到\(10^{-16}s\)的量级了。
因此在1967年召开的第13届国际度量衡大会上,通过了用铯-133原子钟作为国际单位制中秒的定义。
国际单位制是世界上最普遍采用的标准度量系统,有七个基本单位。
随着2019年对质量、电流、热力学温度、物质的量的定义调整,现在所有的基本单位都已经采用物理常量的精确数值来定义了。
| 单位名称 | 单位符号 | 物理量 | 定义 |
|---|---|---|---|
| 秒 | \(s\) | 时间 | 铯-133原子在基态下的两个超精细能级之间跃迁所对应的辐射的9192631770个周期的时间 |
| 米 | \(m\) | 长度 | 光在\(1/299792458\)秒内在真空中行进的距离 |
| 千克 | \(kg\) | 质量 | 由普朗克常数 \(h = 6.62607015×10^{−34}J⋅s (J=kg⋅m^2⋅s^{−2})\)、米和秒所定义 |
| 安培 | \(A\) | 电流 | 由元电荷\(e=1.602176634×10^{−19}C (C=A⋅s)\)和秒所定义 |
| 开尔文 | \(K\) | 热力学温度 | 由玻尔兹曼常数\(1.380649×10^{−23}J⋅K^{−1} (J=kg⋅m^2⋅s^{−2})\)、千克、米和秒所定义 |
| 摩尔 | \(mol\) | 物质的量 | 1摩尔包含\(6.02214076×10^{23}\)个基本实体,即阿伏伽德罗常数 |
| 坎德拉 | \(cd\) | 发光强度 | 频率为\(5.4×10^{14}\)赫兹的单色光源在特定方向辐射强度为\(\frac{1}{683}W/sr\)时的发光强度 |
时间的对称性
从生活常识出发,已经建立了一条“时间轴”的概念。现在请想一想什么是“规律”?什么是“物理规律”?
书面意思是“规律是在某种范围内或某种条件下,事物间的必然本质联系”,而物理规律就是物质世界的规律了。
显而易见,物理规律应该是不随着时间而变化的,否则这就不能叫做“规律”了。
这里揭示了时间一个很重要的性质——时间平移不变性:在不同的时间,物理系统服从的规律是相同的。
这句话简直就是把“物理规律”的本意换了一种说法而已,所以这个性质是非常非常基本的,甚至都不能去怀疑它的正确性。
有意思的是,数学上可以证明“诺特定理”:通俗的说,每一种对称性都对应着一个守恒量。
时间平移不变性恰恰就是对应了能量守恒定律,也就是说如果有一天你想推翻一些“老旧”的物理定律,能量守恒是一定要保留到最后的。
另一方面,也可以定义时间反演不变性:例如在牛顿第二定律\(𝑚𝑑^2𝑟/𝑑𝑡^2 =𝐹\)中,将时间反号(\(t'=-t\)),其实完全不会改变运动方程。
也就是说从力学的角度,如果时间方向反过来的话,物理规律应该也是不变的。
但热力学第二定律否定了这一点,也就是说时间其实有一个“正确”的方向,即让孤立系统的熵增大的方向。
一个在动力学规律上满足时间反演不变性的微观系统,为什么在宏观上却不满足时间反演不变性了呢?这仍然是现代理论物理中一个很有哲学意味的问题。
时间的相对性
这里我不打算去思考时间的绝对性问题,也就是说从始至终都没有假设过每个人的时间会是一样的。
请直接进入到“正确”的思维中来,即每个人的时间理应是不一样的。这个性质在物理上被称为时间的相对性。
首先每一个“观察者”可以建立一个参考系,即让我们想象以某某的视角来观察这个世界。所以如果切换观察者的视角,能够看到的世界当然并不一定是一样的,理当如此对吧。
如果想象以一个刚体,即物理假设不会形变的物体,作为参考系。这样就可以用它的前后、左右、上下建立坐标系\(O(x,y,z)\),而空间只有三个方向,这也是来自“生活常识”。
有了坐标系就可以给这个观察者“世界”中的所有物体赋予一个空间坐标了,这里需要引入“长度”的概念。
在思维实验上,只需要用一把“尺子”一点点地在三个方向去丈量,就可以得到某个点在当前参考系下的坐标。
那关键的问题就是,如何“统一”参考系的时间呢?
可以想象,观察者自己手里拿着一个时钟,滴答滴答地在走动。
离观察者很远、但是在空间上保持静止的某一个物体上也有一个时钟。
因为空间是均匀的,观察者和物体在理论上其实是完全对等的地位、彼此可以互相切换,所以在这里可以假设,两者时间流逝的速度理应是相同的。
这里相当于设想两个时钟是同一批次生产的、完全一模一样,所以在时间计数上也就完全相同。
唯一的问题是,两个时钟最初的时刻可能不一定是对齐的。例如在参考系的统一时间里,A时钟是从9点走到了10点,但B时钟是从9点零5分走到了10点零5分,两个时钟有5分钟的时差。
这时候观察者就需要首先和其他空间点上的时钟进行一次时间对齐了。
一个可行的方式就是通过某种信号传输手段(例如“光”),在观察者的时间(如\(t_0=9:00:00\))发送到空间点A,A在收到信号后马上把自己的时间(\(t_1=9:05:01\))发回观察者,当观察者收到返回的消息时(\(t_2=9:00:02\)),马上就可以计算出物体和自己之间的时间差(\(\Delta t=t_1-t_0-(t_2-t_0)/2\)),并由此认为所有空间点都可以与自己进行时间对齐了。
接下来,继续考虑两个有相对运动的参考系。按照上面的方式,首先两者都可以分别建立自己的时空坐标系\(O(x,y,z,t)\)和\(O^{\prime}(x^{\prime},y^{\prime},z^{\prime},t^{\prime})\)。
为了方便,前者一般称为“静止系”,后者称为“运动系”。需要注意的是,静止和运动在这里是相对的,所以完全等价地,也可以把后者当做静止系,而把前者当做运动系。
在分清两个参考系后,就容易理清“同时”的相对性问题了。
“同时”可以有两种表述,一是在同一个地点同时发生了两个事件,但是更广泛地是在不同的地点同时发生了两个事件。
例如一个人站在窗边,外面电闪雷鸣,有两道闪电的光同时从左右两边射了进来,过了几秒它们的雷声也同时响起,那在这个人看来这两次闪电应当是同时发生的。
对于一个参考系来说,例如在静止系中,A和B同时的意思就是事件在时空坐标上满足\(t_A = t_B\)。
因为在两个相对运动的参考系中,建立了不同的时空坐标系,即一般来说\(t_A \neq t^{\prime}_A\)且\(t_B \neq t^{\prime}_B\),所以对于静止系中同时的事件,在运动系中当然并不一定也是同时的了。
狭义相对论
首先狭义相对论只讨论惯性系中的物理问题,也就是静止参考系和与静止系保持匀速直线运动的参考系。
引入两条简单的基本原理:
- 光速不变原理:在所有惯性系中,真空中的光速不变,且与光源运动无关
- 狭义相对性原理:在所有惯性系中,物理定律有相同的表达形式。
光速不变的思想来自于19世纪末的大量物理实验,最终被爱因斯坦敏锐地提升到了原理的高度。
相对性原理通俗地说,就是在不同的惯性系中,物理公式在形式上应该是一样的,比如静止系里的公式如果是速度的一次方,到了运动系里就不应该变成了速度的二次方。
如果预先接受麦克斯韦方程组是正确的,在相对性原理的基础上,也可以根据真空介电常数和真空磁导率两个自然常量推导出光速不变性。
但是需要强调的是,狭义相对论并不依赖麦克斯韦方程是否正确,也就是说光速不变仍然是狭义相对论中一个独立的基本原理。
从狭义相对论的两条基本原理出发,我们可以推导出两个有相对运动参考系之间在时空坐标系上的变换关系。
在牛顿的绝对时空观中,即满足伽利略变换:
\(x^{\prime}=x-vt\)
\(y^{\prime}=y\)
\(z^{\prime}=z\)
\(t^{\prime}=t\)
其中\(v\)是参考系之间的相对速度,可以看到绝对时空观里,假设了两个参考系可以有完全相同的时间。
而在狭义相对论中,即满足洛伦兹变换:
\(x^{\prime}=\frac{x-vt}{\sqrt{1-v^2/c^2}}\)
\(y^{\prime}=y\)
\(z^{\prime}=z\)
\(t^{\prime}=\frac{t-\frac{vx}{c^2}}{\sqrt{1-v^2/c^2}}\)
其中\(\gamma=1/\sqrt{1-v^2/c^2}=1/\sqrt{1-\beta^2}\)称为洛伦兹因子,又名相对论因子,在相对论的公式中可以经常见到。
爱因斯坦在讲解相对论时,喜欢将静止系称为地面参考系,而把运动系看做一辆匀速行驶的火车,即火车参考系。
想象在火车上,从车底垂直向车顶发射一道光线。
根据光到达车顶的时间,可以得到车厢的高度是\(c\Delta t^{\prime}\),其中\(c\)是光速,\(\Delta t^{\prime}\)是火车系里的时间。
在地面系看来,因为火车在运动,这道光线就不是垂直向上而是斜着地走了\(c\Delta t\),注意到这里运用了光速不变原理,\(\Delta t\)是地面系的时间,而且在这个时间里在地面系看到火车也移动了\(v\Delta t\)的距离。
在地面系看来,火车移动的距离、车厢高度和光线斜着运动的长度构成了一个直角三角形。
根据勾股定理,就可以得到\((v\Delta t)^2+(c\Delta t^{\prime})^2=(c\Delta t)^2\),即\(\Delta t=\Delta t^{\prime}/\sqrt{1-v^2/c^2}=\gamma \Delta t^{\prime}\)。
这里不仅得到了相对论因子,而且因为\(\gamma > 1\),可以看到在地面系看来,它的时间\(\Delta t\)走得比火车上的时间\(\Delta t^{\prime}\)要快,或者说地面系认为火车上的时钟走得比地面的时钟要慢,也就是“动钟变慢”的效应。
狭义相对论还可以得到一个重要的公式——质能方程:
\(E=mc^2\)
这里的质量\(m\)是物质的动质量,会随着物体的运动速度变大而变大。
一个有静止质量的物体在加速到光速后,能量会变成无穷大的,预示了光速是物质世界的最大速度。
狭义相对论的效应
首先动钟变慢可以“合理”地解释中国古代神话故事,例如西游记里说的“天上一日、地上一年”。根据\(\gamma = 365\),就可以得到神仙在天上是以\(0.999996\)倍光速在运动的。:)
除了动钟变慢的效应,狭义相对论还带来了“动尺缩短”的效应。例如,在地面系测量火车车厢的长度,会比火车系自己测到的车厢长度要短。
动尺缩短与同时的相对性有重要的联系。
因为测量长度最重要的是能够“同时”测得两个端点的空间坐标,而在地面系看来,火车系自己测量车厢的时候不是“同时”的,所以自然两个参考系所测量得到的长度也就是不一样的。
动钟变慢和动尺缩短也“提醒”了我们保持运动的重要性,因为运动可以让人活得更久、变得更瘦哦。:)
另一方面,初次认识相对论的人也会有很多困惑,比如其实明明可以发现很多的“超光速”现象。
用一支激光笔,假设它的光照射到了月球上,可以想象只要手轻轻地转动,在月球上的光斑就会非常快速地移动,甚至超过光速。
但这种“影子”式的超光速,并不与相对论有任何冲突,因为这里真实运动的物质“光”仍然是在保持光速运动的。
再比如我们在运动场看台上表演的“人浪”,如果大家配合出色,这个波浪围着运动场的传播速度也可以是非常快的,但是真实的观众只是原地站起来又坐下而已,当然没有发生真实物质上的“超光速”。
借用后来信息论的语言,其实狭义相对论表达了“信息”的传播速度是不可能超过光速的。
如果发生了超光速,就会对因果律的哲学产生颠覆。
因果律就是事件发生的因果关系,比如母鸡生小鸡,有因才有果。
用事件的语言来描述因果律,就是A事件的发生可以传递出来一种信息,这个信息的传播速度不会超过光速,而信息最终引发了B事件。
在科幻中,如果有某种超光速的能力,那在B事件发生时,就可以传递另一个信息回到A事件发生前,从而阻止了A事件的发生,这就是“外祖母悖论”。
从因果律的角度,一个观察者只能观察到一段时间内光速可传播范围内的事件,即以观察者为时空原点,可观察到的事件坐标要满足\(x^2+y^2+z^2 \leq c^2t^2\),这在四维时空中是一对“圆锥”,称为光锥。
在狭义相对论中,光锥表示的是与当前事件能够存在因果关系的所有时空点的集合,包括了过去光锥和未来光锥。
狭义相对论的应用
在20世纪初,爱因斯坦提出相对论之后,相对论特别是狭义相对论已经成为了现代物理学的基石。
在大众看来,可能觉得相对论离我们的生活还很遥远,但其实在现代生活中需要运用相对论的地方无处不在。
例如我们日常使用的定位服务,包括美国的GPS、中国的北斗等卫星导航系统,就离不开相对论的应用。
卫星导航系统的原理是用多个卫星发出的时空坐标,在接收器上通过“三角运算”来计算出所在点的坐标(经度、纬度、海拔高度以及时间)。
所以一般来说至少需要三颗卫星才能确定一个空间定位,当然如果能连接到的卫星越多,可以达到的精度就会越高。
因此导航卫星上都需要安装一个高精度的原子钟用于计时。
但是卫星在围绕地球运动,也就会产生“动钟变慢”的相对论效应。
现在来计算一下原子钟的时间漂移,即其引起的定位误差。
一般来说,导航卫星的高度大约2万公里,相应的速度大约为\(4km/s\)。
因此狭义相对论效应带来的“相对误差”为\(\Delta = \gamma - 1 \approx v^2/2c^2 \approx 10^{-10}\)。
也就是说,导航卫星如果每绕地球一周(大约12小时),就会因为“动钟变慢”的效应带来约4微秒的误差,乘以光速即对应了大约1200米的定位偏移。
所以如果现代卫星导航系统的定位精度是这么差的话,肯定就无法实用了。
广义相对论
狭义相对论是限定在惯性参考系里的讨论,如果是非惯性参考系呢?
这个问题要复杂得多,但爱因斯坦在发表狭义相对论之后十年就又发表了广义相对论。
广义相对论引入了“等效原理”,即非惯性系中感受到的惯性加速度是与万有引力的重力加速度在效果上是完全等效的,或者说作为引力“荷”的引力质量与力学中代表惯性的惯性质量是完全等效的。
可以想象,在一片没有任何天体的空间有一个静止的观察者A,同时有一个加速运动的电梯里面有观察者B。
在A看来因为电梯向上加速运动,B会受到一个虚拟的、向下的惯性力,而在B看来电梯是静止的,但是自己受到了一个持续的、向下的力,可以等效为电梯地面的“引力”,虽然电梯下方并没有真实的天体存在。
所以在电梯内部放下一个苹果,在观察者B看来也会和万有引力一样苹果加速落到地上。
等效原理确保了在一个封闭的电梯内,观察者是没有办法通过物理实验来判定自己到底是处于一个加速运动的空间里,还是处于一个引力场之中。
从广义相对论引申出,有质量的时空不是平直的、而是弯曲的,也就是说前面狭义相对论中认为不同空间点的时间流逝速度相同(平直时空)是不准确的。
广义相对论“意外地”统一了时空和引力,即引力其实是时空弯曲的几何效应。
对于时间来说,广义相对论可以带来称为引力红移的效应,也就是在引力场越强的地方,时间流逝就越慢。
例如利用两个非常精确的原子钟,可以测量发现海拔450米左右的东京晴空塔上时间每天比地面快4纳秒。
对于导航卫星来说,因为引力红移的效应,每天要快大约45微秒。
相比于每天慢约8微妙的狭义相对论“动钟变慢”的效应,导航卫星要考虑的广义相对论影响明显更为重要。
时间是连续的吗?
在相对论中时间是连续的,但另一个现代物理学的支柱——量子理论,给世界带来了离散性。
根据广义相对论和量子理论,可以得到一个普朗克时间\(𝑡_𝑝=(\hbar 𝐺/𝑐^5)^{1/2}=5.4×10^{−44}s\),这是现代物理学在理论上有效的最小时间尺度。
这对应着普朗克长度\(l_𝑝=(\hbar 𝐺/𝑐^3)^{1/2}=1.6×10^{−35}m\)和普朗克能量\(E_𝑝=(\hbar 𝑐^5/G)^{1/2}=1.22×10^{19}GeV\)。这里\(GeV\)是一个能量单位,即\(10^{9}\)电子伏特。现在世界最大的大型强子对撞机(LHC)的能量也才到\(TeV\)量级,也就是\(10^{12}\)电子伏特。
从宇宙大爆炸假说出发,时间是存在一个“原点”的,也就是说在基础理论上,普朗克时间之外的宇宙所遵循的基本物理规律差不多已经被人类掌握了。
也就是说,在某种意义上,我们可以“准确地”推演出宇宙大爆炸后,质子等各种粒子的形成,氢氦等更多原子的形成,恒星的诞生,银河系等星系的诞生,直到现在所看到的整个宇宙。
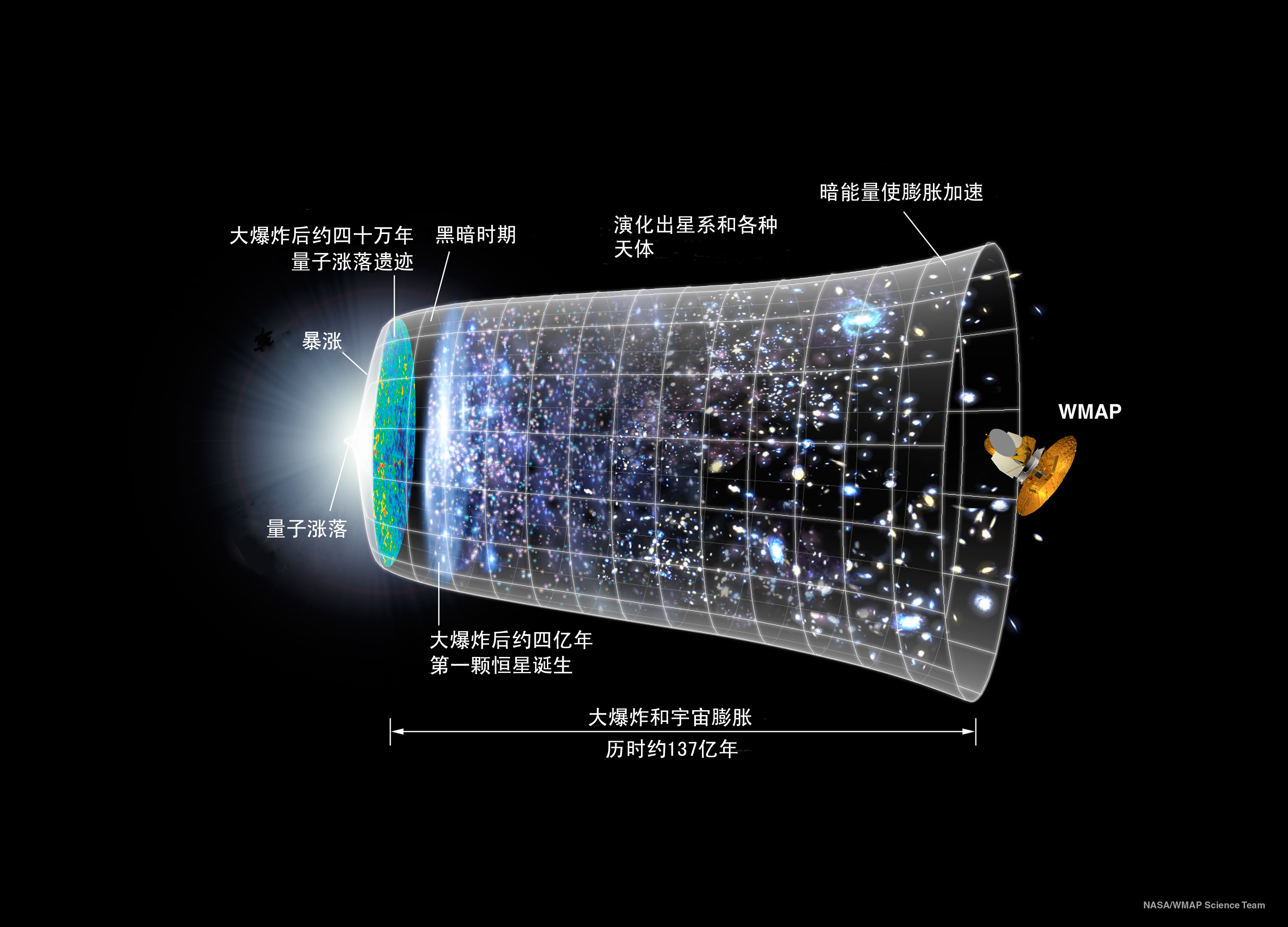
但是,在普朗克尺度下,引力的量子效应将变得非常重要,而物理学上还并没有建立满足量子化的引力理论,也就是说在普朗克时间内,现在已知的所有物理理论是失效的,那里还是一片未知的“时空”。
普朗克时间只是现有物理理论失效的一个时间尺度,真实世界的时间是否可以继续细分甚至无限细分呢?我们并不知道。
所以在物理世界里,用数学表示的时间虽然形式上很简单,只是一条被称为时间轴的线,但是还没有人确定,这条线到底是连续的点、或者是离散的点所组成的。
虚拟时间
数字时代搭建起了虚拟世界
计算机里的时间
计算机是用数字电路组成的。在数字电路里的一切运算都要按时钟频率来工作。
所以没有时钟,数字电路就无法工作。
例如一段电流信号,必须按照时钟周期,在相应的时间间隔内以“关”代表0,以“开”代表1。
在每一台现代计算机中都有“时钟”进行授时。
首先是通过硬件时钟RTC(Real-Time Clock)来记录时刻,RTC是计算机中独立的一块硬件并自带电源,也就是说在电脑关机的情况下仍然可以工作。
RTC会持续记录一个比较粗略的时间,例如某年某月某日某时某分某秒,与电子表计时是类似的。
可以想象,硬件时钟不是特别的精确。例如因为硬件制作工艺不可能完全相同,不同计算机的硬件时间本身就不一样。
另一方面,个人电脑如果长期不使用,硬件时钟因为有计时误差,所以可以发现当再次开机时,电脑显示的时间会与真实世界的时间有比较大的差异。
不过,计算机显示的时间不是直接来自硬件,而是由操作系统提供的。
操作系统会通过硬件和软件提供一个“时钟”,称为操作系统时钟。
例如,操作系统会在开机时获取硬件时钟的时刻,再利用CPU计时器等记录程序运行的时段,从而得到一个实时的时间。
既然不同的计算机会有不同的时钟,为了统一全球计算机的时间,就需要一个标准时间来实现时间同步。
网络时间协议(NTP)就是用来使计算机时间同步化的一种协议,可以提供高精准度(毫秒级)的时间校正。
所以在实际上,操作系统会通过网络时间协议获取网络时间,并对当前计算机的时间进行校正,这样我们才能始终在自己电脑上看到跟“真实时间”一致的数字时间了。
可以设想,如果电脑长时间不联网,它的时间也会发生“漂移”。
这就是有时候在一些内部网络环境中,可以发现实时的调用请求与互联网时间存在“时差”的原因。
另外,位于陕西西安的中国科学院国家授时中心,承担着我国国家标准时间(北京时间)的产生、保持和发播任务,所以新闻联播在每天晚上7点播报的,其实是来自西安的“北京时间”。
计算机时间的表示
一般在计算机中表示时间有两种常见的格式,一种是Unix时间戳。
Unix时间戳是一个有符号的整数,记录了世界协调时(UTC)时间上自1970年1月1日0时0分0秒以来的总秒数或总毫秒数。
例如世界时的1970年1月1日0时0分0秒就是0秒,北京时间的2022年2月2日22时22分22秒就是1643811742秒。
另一种格式是国际标准化组织制定的ISO-8601时间格式,可以比较友好地表示时间。
例如世界时的2022-02-02T22:22:22Z,北京时间(东八区)的2022-02-02T22:22:22+08:00。
目前看起来,时间在计算机中好像还是比较简单的。
但是其实时间表示还是带来了很多意想不到的问题,也就是程序bugs。
例如著名的千年虫问题:上个世纪囿于存储空间有限,再加上人们普遍觉得系统更新会很快,所以程序员大多采用两位数来表示年份,比如用06/15/98,而不是06/15/1998。但是当进入新世纪,到了2000年,系统只知道是01/01/00,不知道这是1900还是2000,就发生了程序错误。
类似千年虫的问题还有很多,例如早期计算机采用32位系统,时间戳也只使用了32位有符号整数,这样能表示的最大正整数是\(2^{31}-1=2147483647\),对应的世界时即2038-01-19T03:14:07Z。也就是说,到了2038年1月19日,如果还有系统在使用32位时间戳的程序,类似千年虫的问题又要出现了。
更加意想不到的是,还有“闰秒”引起的bug。
因为原子钟测量得十分精确,我们其实可以发现由于地球自转的不规则和长期的自转减慢等效应,天文观测上的一年不是一个完全不变的周期时间,比如不同的回归年之间可以差出来那么一秒钟。
一般来说多年积累下来,这个差值会是多一秒,但也有可能少一秒,这就要想办法“置闰”到世界的标准时间中去,因此被称为闰秒。
对于到底要不要继续设置闰秒,国际上有很多的讨论,支持一方的主要观点是:如果不对闰秒进行任何处理,我们未来使用的计时系统就会与看到的自然现象不吻合了。
例如很多很多年以后,可能时钟显示早上8点,起床才发现太阳其实正在下山,因为精确的计算机时间与缓缓变化的自然周期时间之间在不断积累差异。
在2012年6月30日,当时UTC时间上插入了一个正闰秒。
不幸的是,由于Linux系统某些版本的闰秒处理逻辑,触发了一个死锁的bug,造成了大规模的Linux服务器内核死锁而宕机。
简单地说,Linux内核在处理闰秒时会先进行时钟中断,这里会给时钟加锁,而处理过程中会调用打印函数来记录日志。
不巧的是打印函数中本身又需要调用时钟,但是因为时钟已经加锁而且无法释放,最终就造成了内核死锁而整个系统宕机。
可以看到,与时间有关的问题所造成的软件缺陷是非常隐蔽、难以发现的,上面几个例子也体现出来很多的“意想不到”。所以程序员们,在编程中如果碰到跟时间有关的问题,请一定要多思考一下并保持警惕哦。
例如,假设要实现一个可以自恢复的数据服务,即先将调用请求存入日志缓存,然后再依次处理数据,这样可以在系统断电等意外发生时,就从未处理完成的日志恢复,重新开始处理数据,从而给用户提供一种安全可靠的服务。
一种很直观的实现方式,可能会选择以时间戳作为日志的标识键(或键值的一部分),这样只要在系统重启时搜索中断时间以后的所有日志,重新处理数据就可以了。
但是请别忘了,重启后的操作系统时间是可能发生变化的,甚至以时间戳表示的重启时间有可能还会小于记录的“中断时间”(操作系统时间穿越了),那些未处理的日志则有可能不仅不会被处理,反而会被新的请求给覆盖了。
分布式系统的时间
分布式系统一般是利用网络进行消息传递,在多台计算机设备上实现数据一致性、故障容错性的复杂系统,从而解决服务高可靠高可用、性能瓶颈、设备异地分布等实际问题。
在分布式系统理论中,时间具有重要的意义。
首先如果在多台计算机中可以有且仅有唯一的全局时钟,可以保证在有限时间内完成计算,在有限时间内完成网络传输,被称为“同步系统”。
同步系统中发送出去的消息是有确定的返回时间的,所以只要大多数节点回复了相同的消息,就可以认为整个分布式系统达成了一致。
即在少数服从多数的情况下,同步系统可以提供50%的容错率。
反之称为“异步系统”,即就算本地时钟的差异小到可以忽略不计,但取决于带宽的拥塞程度、CPU的繁忙程度,互相之间发送消息的延迟还是非常地不确定。
在分布式系统理论中,由Fischer,Lynch和Patterson提出了著名的FLP不可能原理:即在网络可靠,存在节点失效(即便只有一个)的最小化异步模型系统中,不存在一个可以解决一致性问题的确定性算法。
也就是说异步系统的容错率是0%。
一个形象的例子是“三个和尚没水喝”:A、B、C每天早上要决定去不去挑水,第一次A说去、B说不去,所以要等C来决定,但C还在睡觉(节点失效);等了一天C睡醒后收到了B的消息决定不去,A还是要去,所以要等B决定,但B等得太久又睡着了;又等了一天B也睡醒了,想了想原本应该听A的所以又选择了去,C还是不去,所以最后还是要等A决定,但A等了两天实在太累了,也睡着了。这样循环往复,也就是说异步系统是不可能可靠的。
但实际情况还没有那么极端,如果系统可以保证在有限时间内完成计算和网络传输,但是这个时间无法被预先知道,或者系统只能在一段无法预知的时间内,保证计算和网络传输有一个时间上限,这样被称为部分同步系统。
因为网络分区等可能性存在,部分同步系统可以实现的容错率是33%。
例如,PBFT算法中可以使用\(3f+1\)节点,来允许\(f\)个节点失效甚至作恶。
既然分布式系统如此复杂,那今天在我们大量采用云服务的情况下,为什么开发分布式系统时,程序也能够运行得好好的?
没有感知并不代表问题不存在或者不重要,程序员使用的很多基础级软件,例如Consul、Kafka或者说分布式系统里一切看似中心化的部分,都已经使用了类似的机制,只不过是有人帮你把这些细节屏蔽掉了而已。
区块链
区块链就是在大量的分布式节点中用一个个区块串起来的唯一链条。
首先区块链网络是有多个区块链节点组成的,每个节点一般不存在谁比谁更特殊的关系,所以称之为对等节点和对等网络。
各个节点在收到对区块链系统的请求(一般称为交易)后,会首先通过数字签名验证交易的真实性,并通过自己的本地账本验证交易的有效性,同时向其他节点进行广播。
通过区块链的共识机制,可以对单笔或多笔交易打包形成的区块达成一致性共识,即多数节点都能认可此区块以及其中全部交易数据的正确性,并最终记入到自己的本地账本中。
区块链中的一个个区块通过哈希算法和哈希值依次串联,这也是区块链(Blockchain)名字的由来了。
所以链上的一个个区块就是一个个的时间戳,标识着这个系统的过去、现在、未来,从而协调整个以区块链为基础的分布式系统在“时间”上步调一致地前进。
可以说“区块即时刻、链即历史”。
在区块链系统中的物理时间概念已经模糊了,因为一般只需要通过区块号的大小,就可以快速辨别系统时间的先后。
例如以太坊在系统更新时,通常都不会指明具体的物理时间,而是以未来的某个区块号作为发版目标。
因此站在当前数字化的“元宇宙”时代,区块链可以说是为虚拟世界建立了一种时间基座。
从物质世界走进虚拟世界,我们的闲聊就到此结束吧,但时间永不停逝。